The slope intercept form is a linear equation used in algebra and analytical geometry to represent the equation of a straight line. It is particularly useful for finding the equation of a line when we know the numerical values of the slope and y-intercept. An equation of a line is one in which all points on that line satisfy the equation. The equation of the line can also be expressed in three other forms.
- Point-Slope Form
- Intercept Form
- Two-Point Forms
The form selection depends on the given information and the desired result. However, the slope intercept form is a popular choice among students due to its simplicity.
We will discuss the definition and formula of the slope intercept form in this article and learn how to derive the equation with many examples to understand this concept clearly.
Definition and Explanation of Slope Intercept Form
The slope-intercept form is a way to find out the straight-line equation in two dimensions. We will need a slope or angle of inclination and y-intercept to find the equation of the straight line through this method. This form is popular because it makes it easy to read off slope and the y-intercept without drawing the line on a graph.
Let us break the slope-intercept concept into two parts.
1. The slope of a Line is defined as the ratio of the change in the y-axis to the change in the x-axis. It is represented by the symbol m.
![]()
2. Y-intercept is a point on the y-coordinate where a straight line intersects the y-axis. The y-intercept coordinates are expressed as (0, b).
Formula for Slope-Intercept of the Line
The following equation of a slope intercept form can be used to evaluate a straight-line equation.
y = mx + b
Here:
- m = slope or steepness of a line.
- b = y-intercept (a point where a line crosses or cuts the y-axis).
- (x, y) = The coordinates of a point lie on a line.
Derivation of Slope-Intercept Equation
Let us learn how to get the equation of the slope-intercept form (y = mx + b).
Consider a line L with a slope m crossing the y-axis at a distance of b units from the origin O.
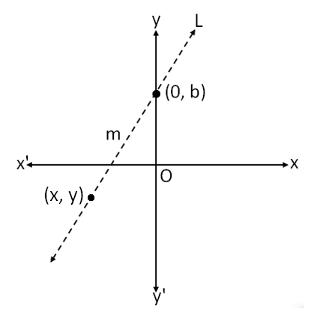
To find the slope of line L that passes through the points (0, b) and (x, y), we will use the slope formula:
∴ m = (y2 – y1) / (x2 – x1)
Place the given values in the equation of slope.
m = (y – b) / (x – 0)
m = (y – b) / (x)
Multiply “x” on both sides.
mx = y – b
Add “b” on both sides of the equation.
mx + b = y – b + b
mx + b = y
(or)
y = mx + b
That is the standard form of the slope intercept.
Converting the General straight-line equation into the Slope-Intercept Form
The equation of slope-intercept can be derived from the general equation of a line in the following way.
The General equation for a straight line is
Ax + By + C = 0
Isolate the value of “y” on one side of the equation.
By = – Ax – C
Divide “B” by each term.
y = (- A/B) x + (- C/B)
That is the form of slope-intercept form.
Here (- A/B) is the slope and (- C/B) is the y-intercept (b) of the line.
Solved Examples of Slope Intercept Form of a Line
Let us understand how to compute the equation of a straight line from its slope-intercept form.
Example 1:
Find the equation of a line with a slope of – 4 and a y-intercept of 2.
Solution:
Step 1: Identify the slope m and y-intercept b of the line.
Given:
Slope (m) = – 4
Y-intercept (b) = 2
Step 2: Use the slope intercept form and place the given values in it.
y = – 4x + 2
That is the required equation of a line.
Example 2:
Write the equation of a line that passes through the point (-2, 5) with a slope of -2.
Step 1: Determine the slope (m) and y-intercept (b) of the line.
Here,
m = -2
(x, y) = (-2, 5)
Step 2: Place the given values in the slope intercept equation to determine b.
5 = -2 (-2) + b
5 = 4 + b
b = 1
Step 3: Now put the value of b and m into the formula of slope intercept form.
y = – 2x + 1
That is the equation of the line that passes through the point (-2, 5) with a slope of -2.
Example 3:
Determine the equation of a straight line that passes from the points (2, 4) and (6, 8).
Solution:
Step 1: Calculate the slope of the given line at first.
m = (8 – 4) / (6 – 2)
m = 4 / 4
m = 1
Step 2: Let us choose the first given point (2, 4) to find the value of b.
∴ y = mx + b
4 = (1) (2) + b
b = 2
Step 3: Place the value of b and m in the slope intercept equation.
y = 1x + 2
This is the equation of the line that passes from the points (2, 4) and (6, 8).
You can also use a slope intercept calculator to solve the problems of finding equation of the line to get the results in couple of seconds.
Conclusion
In this article, we have discussed the introduction of slope intercept form and then we expanded this concept to an advanced level. We have explored the formula for slope-intercept form and learned how to get it. We converted the general equation of a line into the form of a slope intercept. We solved different examples that will help you to determine the equation of the line with ease.
